https://www.youtube.com/watch?v=ffh9hlpj_Qs
1. Einführung
Der Nachweis, dass alle zeitlichen Anforderungen einer Aufgabenstellung unter allen Umständen eingehalten werden können, ist alles andere als trivial. Er ist jedoch wichtig, um theoretisch sicherzustellen, dass z. B. im Falle eines Verkehrsunfalls der Airbag als lebensrettende Maßnahme rechtzeitig aufgeht.
2. Welche Bedingungen müssen geprüft werden?
- 1. Echtzeitbedingung (Auslastung)
- 2. Echtzeitbedingung (Pünktlichkeit)
Gegeben ist ein System mit Rate Monotonic Scheduling. Darauf laufen die folgenden Prozesse:
\(P1\): Verarbeitungszeit \(10\)ms, Zykluszeit \(30\)ms
\(P2\): Verarbeitungszeit \(15\)ms, Zykluszeit \(45\)ms
\(P3\): Verarbeitungszeit \(15\)ms, Zykluszeit \(60\)ms
Bei allen Prozessen ist die maximale zulässige Reaktionszeit \(t_{\text{max}}\) so lange wie die Zykluszeit \(T_k\).
3. Nachweis der 1. Echtzeitbedingung
Die Gesamtauslastung des Systems darf maximal \(100\%\) betragen. $$\sum\limits_{k=1}^{n}{\dfrac{C_k}{T_k}}\leq 1$$ Dabei ist \(C_k\) die Verarbeitungszeit von Prozess \(k\) und \(T_k\) die Zykluszeit von Prozess \(k\). Da auf dem System \(3\) Prozesse laufen, ist \(n=3\) und du berechnest:
$$\sum\limits_{k=1}^{3}{\dfrac{C_k}{T_k}}=\dfrac{10}{30}+\dfrac{15}{45}+\dfrac{15}{60}=\dfrac{1}{3} +\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{11}{12}\lt 1\text{ }\surd$$ Da der errechnete Auslastungswert
kleiner als \(1\) (\(100\%\)) ist, hast du die erste Echtzeibedingung erfolgreich nachweisen können.
4. Nachweis der 2. Echtzeitbedingung
Die zweite Bedingung nachzuweisen ist schon weitaus komplexer. Eine gute und nachvollziehbare Möglichkeit bietet hier die graphische Lösung. Dabei ist \(C(t)\) die noch zu erbringende Rechenzeit. Du gehst dabei wie folgt vor:
1. Bei \(t=0\) addierst Du die Verarbeitungszeiten aller Prozesse.
2. Du zeichnest eine Strecke mit der Steigung \(-1\) vom Schnittpunkt mit der \(y\)-Achse bis zu dem Zeitpunkt, an dem ein anderer Prozess die Verarbeitung starten möchte (ergibt sich aus der Zykluszeit). Dies ist erstmalig bei \(t_1=30\) (Prozess \(1\)) der Fall. Es können zu einem bestimmten Zeitpunkt auch mehrere Prozesse gleichzeitig starten wollen.
3. An diesem Punkt addierst du die Verarbeitungszeit des Prozesses (bzw. der Prozesse) und erhältst eine Verschiebung in \(y-\)Richtung.
4. Diese Schritte (Strecke zeichnen, Verarbeitungszeiten der Prozesse an den entsprechenden Punkten addieren, ...) führst du nun so lange weiter, bis du den ersten Schnittpunkt mit der \(t-\)Achse erhältst.
Graphisch sieht das Ganze dann wie folgt aus:
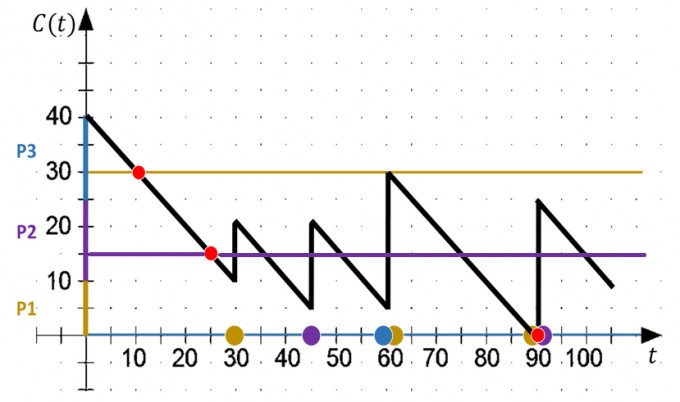
Nun zeichnest du Parallelen zur \(t-\)Achse, die sich durch eine Verschiebung in positive \(y-\)Richtung um die Verarbeitungszeit des Prozesses ergibt, für den die Reaktionszeit bestimmt wurde. Auf diese Weise kannst später die tatsächlichen Reaktionszeiten ablesen. Der jeweils erste Schnittpunkt (von links aus gesehen) mit dem schwarzen Graphenverlauf ergibt die (tatsächlichen) Reaktionszeiten für den Prozess \(2\) (Schnitt mit der violetten Parallelen) und \(1\) (Schnitt mit der dunkelgelben Parallelen).
Nun musst Du nur noch die graphisch ermittelten tatsächlichen Reaktionszeiten mit den maximal zulässigen Reaktionszeiten vergleichen. Man sieht, dass die tatsächliche Reaktionszeit von Prozess \(3\)
bei \(90\)ms und somit über der maximal zulässigen Reaktionszeit (\(60\)ms) liegt. Damit ist die zweite Echtzeitbedingung <a style="color:rgb(182,95,0)"><b>nicht erfüllt</b></a>!
Autor: Florian André Dalwigk
Dieser Artikel hat 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.