Hallo,
meine Frage ist, ob ich den DFA mit der Sprache L = (ab ∪ b)*(aab)* richtig gezeichnet habe.
LG
nein - wohl nicht, da bei Dir z.B. die Sequenz "aaaaaaaab" möglich wäre, was der reguläre Ausdruck nicht hergibt. Umgekehrt ist nach dem regulären Ausdruck z.B. ein "bbbbbbbaab" möglich, was wiederum in dem DFA nicht berücksichtigt wird.
IMHO sollte dem regulären Ausdruck "(ab|b)*(aab)*" dieser DFA entsprechen:
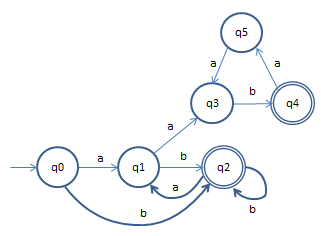
Tipp: sobald zweimal hinter einander ein 'a' erscheint, befindest Du Dich im zweiten Teil -> "(aab)*".
Danke für deine Anwort mit welchem Programm zeichnest du die Automaten?
MS Powerpoint
AH noch was müsste nicht von q4 noch nach q2 eine verbindung sein ? Was wäre wenn bei q4 noch ein zusätzliches b kommt? zb aabb
Nein - eben genau nicht. Wenn der Automat bei q4 angekommen ist, so ist doch bereits mindestens eine Sequenz von "aab" eingetroffen. Man befindet sich also schon im zweiten Teil des regulären Ausdrucks.
Danach werden nur noch weitere Tripel "aab" oder Ende akzeptiert. Der erste Teil des regulären Ausdruck "(ab| b)*" ist bereits abgearbeitet und darf sich an dieser Stelle nicht noch mal wiederholen.
Dann ist die Sache nicht mehr zu retten. Da müsste noch so eine Art Fehlerzustand hin, aus dem man nicht mehr rauskommt .
Das kommt darauf an, was Du mit dem DFA bezweckst; bzw. wie Du ihn darstellst. Sollte in einem Zustand ein Ereignis (hier ein Zeichen) eintreffen, was da nicht vorgesehen ist, so passiert entweder nichts oder der Automat geht in einen (globalen) Fehlerzustand. Das ist Sache der Vereinbarung des Kontextes in dem der DFA benutzt wird.
Im Allgemeinen wird man nicht bei jedem Zustand alle möglichen Ereignisse einzeichnen wollen. Das überlädt so eine Zeichnung völlig.
Ok verstehe das heißt dann es wäre ein toter zustand, so nennen wir das.
@ Werner-Salomon
Dein Automat (a) hat einen Fehler, und (b) kann vereinfacht werden.
.. kannst Du mir bitte einen Tip geben, wo der Fehler liegt. Ich komme nicht drauf.
Kann der fehlerhafte Automat vereinfacht werden? wenn ja - wie?
Z.B.:
Von q0 geht a nach q1 und b nach q2. Das Gleiche hast Du auch von q2 aus, damit ist q0 überflüssig und q2 Dein Start.
Dein Automat muss gar nichts erzeugen, die Definition lässt auch \( \varepsilon \) (= leer) zu. Das Problem lässt sich gleichzeitig mit obigem lösen, da q2 dann sowohl Start als auch Ende ist.
Stimmt - den leeren Ausdruck habe ich ganz vergessen!
Gruß Werner
Ich glaube nicht; denn müsste nicht auch das Wort baab akzeptiert werden.Nur, wenn du mit dem ersten b nach q2 gekommen bist, geht es ja gar nicht mehr weiter.Du musst noch Nachfolgezustände für q2 definieren.
Ein anderes Problem?
Willkommen bei der Stacklounge! Stell deine Frage einfach und kostenlos
