Wie implementiere ich folgende boolsche Funktion mithilfe eines 8:1-Multiplexers?

Question

Frage:

Wie implementiere ich folgende boolsche Funktion mithilfe eines 8:1-Multiplexers?

$$ f = (\neg a \land b \land \neg c) \lor (a \land b \land \neg c) \lor (a \land b \land c)$$

Also wie würde die Wahrheitstabelle für die obige Funktion ausschauen? Es soll ziemlich einfach sein, aber ich verstehe es einfach nicht. Ein 8:1 Multiplexer hat 8 Eingänge, welche man mit 3-Bits theoretisch codieren könnte und die Steuerelemente entscheiden welcher Eingang als Output genommen wird. Soweit so gut, aber wie schaut die Wahrheitstabelle nun entsprechend aus? Ich verstehe es einfach nicht. Ich denke, würde ich die Wahrheitstabelle sehen, würde ich es nachvollziehen können.

Vielen Dank für eure Hilfe!

Answer 1

Die Wahrheitstabelle sieht wie folgt aus:

a	b	c	(¬a∧b∧¬c)	(a∧b∧¬c)	(a∧b∧c)	(¬a∧b∧¬c)∨(a∧b∧¬c)	f = (¬a∧b∧¬c)∨(a∧b∧¬c)∨(a∧b∧c)
0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0
0	1	0	1	0	0	1	1
0	1	1	0	0	0	0	0
1	0	0	0	0	0	0	0
1	0	1	0	0	0	0	0
1	1	0	0	1	0	1	1
1	1	1	0	0	1	0	1

Damit solltest du jetzt in der Lage sein die boolsche Funktion mit einem Multiplexer zu implementieren.

Comments

Danke dir, habe die Aufgabe falsch verstanden. Jetzt habe ich sie richtig verstanden, aber eine Frage hätte ich noch: Wäre es möglich diese Funktion mithilfe eines 4:1 Multiplexer zu realisieren? Wie würde die Wahrheitstabelle ausschauen? Die 4 Eingänge kann man ja mit nur 2 Bits codieren. Hättest du eine Idee?

---

Vielleicht so?

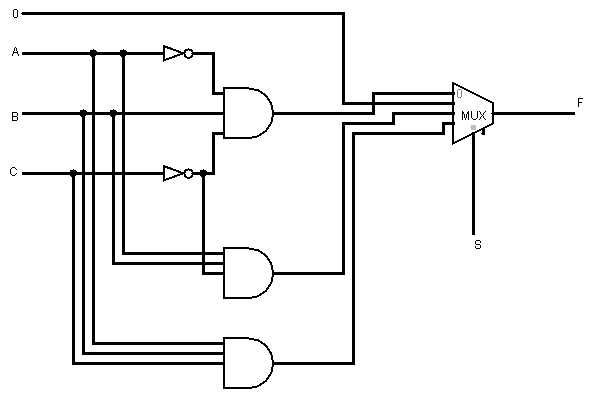
In der Wahrheitstabelle also nur die Bit Werte für a und c betrachten (da b in jedem Term = 1 sein muss), damit S für den Multiplexer bestimmen.

(¬a∧b∧¬c) = 00, a = 0, c = 0

(a∧b∧¬c)  = 10, a = 1, c = 0

(a∧b∧c) = 11, a = 1, c = 1

Und für den I_1 Eingang des Multiplexers 0 als Konstante.

---

Ich denke ich habe es verstanden, danke!