Frage:
Speicherbedarf einer rekursiven Funktion ermitteln.
Wie kommt man auf den Speicherbedarf Cn = 8 ∗ (ln n) + 1? Bzw. was ist der Speicherbedarf von f(x,n)?
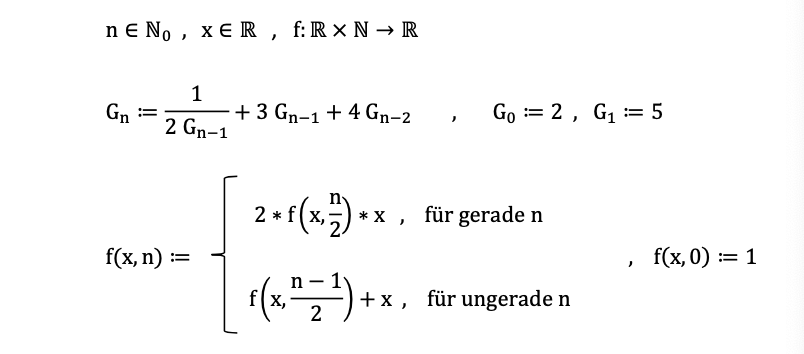
Text erkannt:
\( \mathrm{n} \in \mathbb{N}_{0}, \mathrm{x} \in \mathbb{R} \), f: \( \mathbb{R} \times \mathbb{N} \rightarrow \mathbb{R} \)
\( \begin{array}{l} \mathrm{G}_{\mathrm{n}}:=\frac{1}{2 \mathrm{G}_{\mathrm{n}-1}}+3 \mathrm{G}_{\mathrm{n}-1}+4 \mathrm{G}_{\mathrm{n}-2} \quad, \quad \mathrm{G}_{0}:=2, \mathrm{G}_{1}:=5 \\ \mathrm{f}(\mathrm{x}, \mathrm{n}):=\left\{\begin{array}{ll} & 2 * \mathrm{f}\left(\mathrm{x}, \frac{\mathrm{n}}{2}\right) * \mathrm{x}, \text { für gerade } \mathrm{n} \\ & \mathrm{f}\left(\mathrm{x}, \frac{\mathrm{n}-1}{2}\right)+\mathrm{x}, \text { für ungerade } \mathrm{n} \end{array} \quad, \mathrm{f}(\mathrm{x}, 0):=1\right. \end{array} \)
Text erkannt:
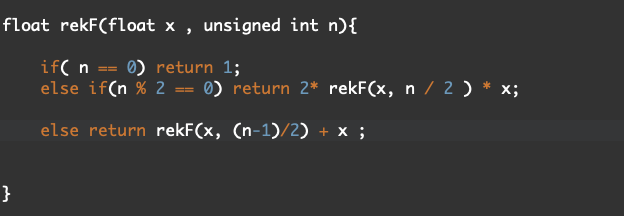
float rekF(float \( \mathbf{x} \), unsigned int \( \mathbf{n})\{ \)
\( \begin{array}{l}\text { if }(\mathbf{n}=0) \text { return } 1 \text {; } \\ \text { else if }(\mathbf{n} \% \quad 2=0) \text { return } 2^{*} \operatorname{rekF}(\mathbf{x}, \mathbf{n} / 2) * \mathbf{x} \\ \text { else return } \operatorname{rekF}(\mathbf{x},(\mathbf{n}-1) / 2)+\mathbf{x} ;\end{array} \)
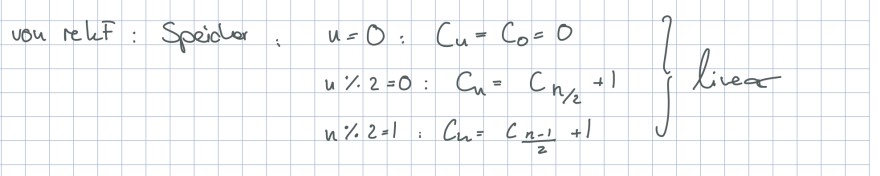
Text erkannt:
vou relef: Speidul: \( \left.\begin{array}{rl} & u=0: C_{u}=C_{0}=0 \\ & u \% 2=0: C_{u}=C_{n / 2}+1 \\ & u \% 2=1: C_{u}=C_{\frac{n-1}{2}}+1\end{array}\right\} \) livea

Text erkannt:
Anmerkungen:
- \( \log \mathrm{n}=\log _{10}(\mathrm{n}) \)
- Wenn bei der Implementierung von \( \mathrm{f}(\mathrm{x}, \mathrm{n}) \) kein Speicherbedarf ermittelt wurde, kann \( C_{n}=8 *(\ln n)+1 \) verwendet werden.
Code: