Aufgabe 4 (2+1+2+2=7 Punkte)
Es sei \( A=\{0,1\} \) ein Alphabet. Für jedes \( n \in \mathbb{N}_{0} \) sei \( V_{n}=A^{n} \) sowie \( E_{n} \) die Menge
\( \left\{\left\{w_{1}, w_{2}\right\} \mid w_{1}, w_{2} \in V_{n}\text{ und }\exists i, j \in \mathbb{Z}_{n}:\left(i \neq j \wedge \forall k \in \mathbb{Z}_{n}:\left(k \notin\{i, j\} \leftrightarrow w_{1}(k)=w_{2}(k)\right)\right)\right\} \)
und es sei \( G_{n} \) der ungerichtete Graph \( \left(V_{n}, E_{n}\right) \)
LÖSUNG:
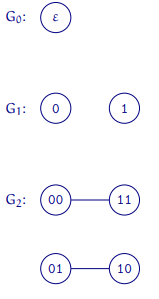
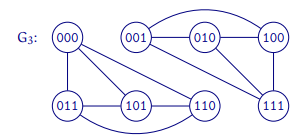
Könnte mir bitte jemand erklären, wie die Kantenmenge gebildet wird?
Mein Versuch:
Z_0 = {}
Z_1 = {0}
Z_2 = {0,1} wähle i = 0 und j = 1 , dann gibt es kein k ∈ Z_n sodass k nicht∈ {0,1} ?????
Z_3 = {0, 1, 2}