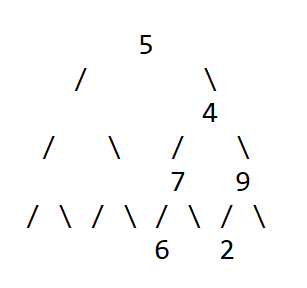Ein binärer Baum kann mit der Methode Preorder oder Inorder dargestellt werden. Die beiden Methoden beschreiben denselben Baum, nur die Reihenfolge der Elemente ist unterschiedlich.
Beispiel:
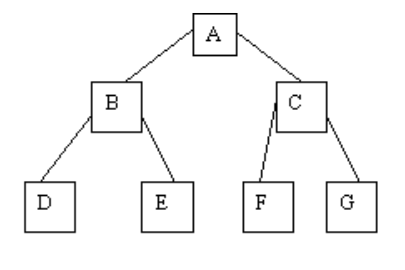
Bei Preorder wird zuerst der Knoten dargestellt, dann der linke und dann der rechte Baum.
A - B - D - E - C - F - G
Bei Inorder wird zuerst der linke Baum dargestellt, dann der Knoten selbst und anschließend der rechte Baum.
D - B - E - A - F - C - G
Die Rekonstruktion wird klar, wenn man sich die beiden Schemata
Preorder: { K,L,R }
Inorder: { L,K,R }
vor Augen führt. "K" ist der Knoten und besteht immer nur aus einer einzigen Zahl. "L" und "R" sind die jeweiligen Äste, wobei die sortierten Mengen Inorder-L und Preorder-L übereinstimmen müssen, ebenso Inorder-R und Preorder-R.
Um diese (unsortierten) Mengen besser zu unterscheiden, schreibt man
Preorder: { K,Lp,Rp }
Inorder: { Li,K,Ri }
Die Mengen Li,K,Ri sind über K eindeutig bestimmbar.
Die Mengen Lp,Rp ergeben sich einfach aus der Anzahl der Elemente von Li und Ri, denn die Anzahl der Elemente muss identisch sein.
Weil Lp und Rp wieder vom Typ { K,L,R } sind, muss das erste Element von Lp/Rp der linke/rechte Kind-Knoten von K sein.
Im nächsten Schritt teilt sich das Schema in zwei unabhängige Äste,
Preorder linker Ast: { K,L,R } = { Lp }
Inorder linker Ast: { L,K,R } = { Li }
Preorder rechter Ast: { K,L,R } = { Rp }
Inorder rechter Ast: { L,K,R } = { Ri }
usw. rekursiv.
_________________________________________________________________________
Aufgabe a)
Preorder 8,5,9,6,3,4
Inorder 3,9,6,8,4,5
K=8
Li=3,9,6 Ri=4,5
Lp=5,9,6 Rp=3,4
Die Mengen Li und Lp (ebenso Ri und Rp) stimmen nicht überein. Fehler !
_________________________________________________________________________
Aufgabe b)
Preorder 5,4,7,6,9,2
Inorder 5,6,7,4,2,9
K=5
Li=leer Ri=6,7,4,2,9
Lp=leer Rp=4,7,6,9,2
Der linke Kind-Knoten von 5 ist leer (Pivot-Element von Lp).
Der rechte Kind-Knoten von 5 ist die 4 (Pivot-Element von Rp).
_________________________________________________________________________
Die neue Preorder (links) ergibt sich aus Lp = leer
Die neue Inorder (links) ergibt sich aus Li = leer
Die neue Preorder (rechts) ergibt sich aus Rp = 4,7,6,9,2
Die neue Inorder (rechts) ergibt sich aus Ri = 6,7,4,2,9
rechts K=4
Li=6,7 Ri=2,9
Lp=7,6 Rp=9,2
Der linke Kind-Knoten von 4 ist die 7 (Pivot-Element von Lp).
Der rechte Kind-Knoten von 4 ist die 9 (Pivot-Element von Rp).
_________________________________________________________________________
Die neue Preorder (links) ergibt sich aus Lp = 7,6
Die neue Inorder (rechts) ergibt sich aus Li = 6,7
Die neue Preorder (rechts) ergibt sich aus Rp = 9,2
Die neue Inorder (rechts) ergibt sich aus Ri = 2,9
links K=7
Li=6 Ri=leer
Lp=6 Rp=leer
Der linke Kind-Knoten von 7 ist die 6 (Pivot-Element von Lp).
Der rechte Kind-Knoten von 7 ist leer (Pivot-Element von Rp).
rechts K=9
Li=2 Ri=leer
Lp=2 Rp=leer
Der linke Kind-Knoten von 9 ist die 2 (Pivot-Element von Lp).
Der rechte Kind-Knoten von 9 ist leer (Pivot-Element von Rp).
_________________________________________________________________________
Der Baum sieht so aus