Beschreibung durch reguläre Ausdrücke

Question

Hallo

es geht um folgende Aufgabe, der Kringel soll hier die Konkatenation sein:

Wenn ich das aber weiterführe  kommt ein so langer Ausdruck raus, dass es einem schwindelt ;)

Das kann man bestimmt besser notieren. Darin bin ich mir aber  sehr unsicher.

Kann ich auch der Art schreiben:

 

?

mfg,

Brausefüralle!

Answer 1

Jeder Regex kann durch einen DFA dargestellt werden. Wenn du dir diesen aufzeichnest, ergibt sich daraus abschreibfertig direkt der reguläre Ausdruck.

* =: Kleensche Hülle,

. =: Konkatenation (Schnitt)

Für L2: ((a + c)* + b) . ((a + c)* + b) . ((a + c)* + b) . (a + c)*

Es ist also sicher gestellt, das genau 3 b im Wort enthalten sind.

Es wird entweder a oder c gewählt, so oft man will. Sobald das erste b gewählt wurde, muss der Automat seinen Zustand ändern um die Eingabe zu erfassen. Danach wiederholt man sozusagen den Schritt noch 2 Mal, eben genau so lange bis die Anzahl von b = 3 ist. Es ist zu jedem Zeitpunkt gewährleistet dass es unendlich viele a und c geben darf, aber nur genau 3 b. Am Ende habe ich noch mal (a + c)* angehängt, damit das Wort nicht nur mit b enden kann.

 

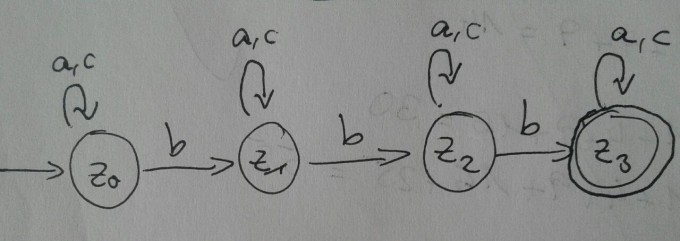
Natürlich kann man viele reguläre Ausdrücke noch vereinfachen, indem man Wiederholungen in den Konkatenationen erkennt, und diese elegant unter einen Hut bringt. Um die Aufgabe formal richtig zu lösen, reicht es aber den DFA in den "erst besten" gültigen Regex um zu schreiben.

Comments

Danke für die Antwort Hansi! Ich denke für L2 habe ich es verstanden. Mal sehen ob ich L3 hinbekomme.

Mein Versuch an der DFA .

So, dazu habe ich jetzt:

L3=

( ((c)* + a) . ((c)* + b) . ((c)* + b) ) + ((c)* + b) . ( ((c)* + b) + ( ((c)* + a) . ((c)* + b)) ) . (c)*

= ( ((c)* + a) . ((c)* + b)²) + ((c)* + b) . ( ((c)* + b) + ( ((c)* + a) . ((c)* + b)) ) . (c)*

Ist das  so okay? Sieht schon wieder so gefährlich  kompliziert aus.;)

mfg

Brause

---

Antwort kommt gleich

---

Konnte leider nicht mehr editieren...

Dein DFA sieht schon ganz gut aus. Du hast die Fälle bb, abb und bab abgedeckt. Es fehlt noch die letzte Möglichkeit mit bba. Das Prinzip hast du aber verstanden ;-)

 

Vergiss nicht den Eingangspfeil bei z₀, da dieser den Automaten seinen Einstiegspunkt wissen lässt =)

---

Mensch, du hast mir echt geholfen! Hätte ich sonst nie hinbekommen :)

 

---

Keine Ursache =)

---

Quadrate dürfen im regulären Ausdruck in der Form übrigens nicht vorkommen. Das zerreist die Struktur des Wortes, da die Buchstaben auf einmal anders angeordnet sind.

Die Konkatenation ist keine Multiplikation sondern die Verkettung zweier Strings, die ihre Reihenfolge zwingend beibehalten müssen.