Ich habe gerade ein Problem.
Und zwar lässt sich ein die Gleichung für ein exlusive or nicht weiter vereinfachen. Sonst wäre es ja nicht mehr das exlusive or.
Nun habe ich diese Gleichung aber mithilfe der Regeln für die boolesche algebra vereinfacht und es kommt E3 raus.
Das kann eigentlich nicht sein. Ich mache einen Fehler, weiß aber nicht wo.
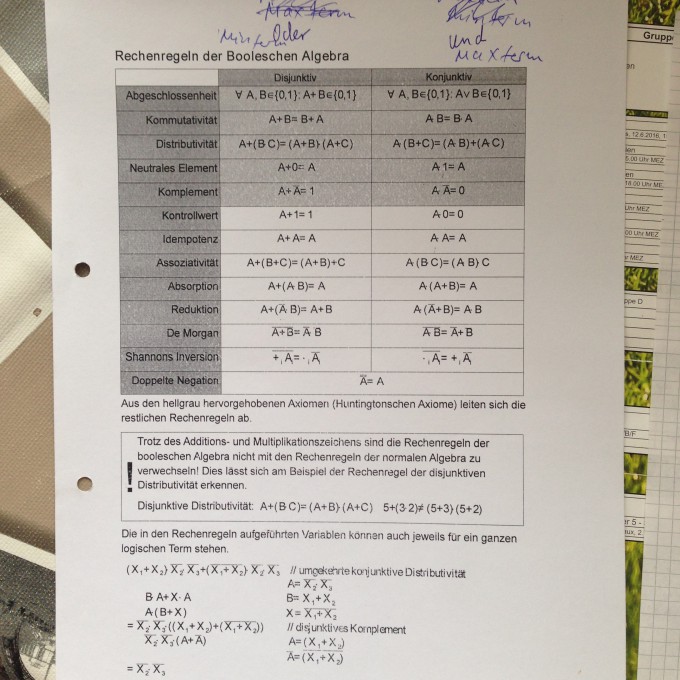
Ich habe meine Rechnung und mein Regelwerk hier als Bild eingefügt.
Bin echt am verzweifeln. Danke im voraus und hoffe hier kennnt sich jemand damit aus.