Frage: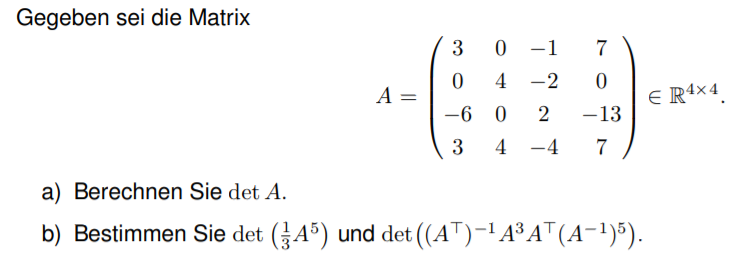
Text erkannt:
Gegeben sei die Matrix
\( A=\left(\begin{array}{cccc} 3 & 0 & -1 & 7 \\ 0 & 4 & -2 & 0 \\ -6 & 0 & 2 & -13 \\ 3 & 4 & -4 & 7 \end{array}\right) \in \mathbb{R}^{4 \times 4} \)
a) Berechnen Sie \( \operatorname{det} A \).
b) Bestimmen Sie \( \operatorname{det}\left(\frac{1}{3} A^{5}\right) \) und \( \operatorname{det}\left(\left(A^{\top}\right)^{-1} A^{3} A^{\top}\left(A^{-1}\right)^{5}\right) \).
Hallo, ich verstehe nicht was ich an b) machen muss, also wie fanke ich damit an?
Code:
