Frage:
Kann mir jemand bitte bitte der Azfgabe helfen, ich schreibe meine Ansätze hin aber habe echt keine Ahnung IV das so stimmt und wie es weiter geht.
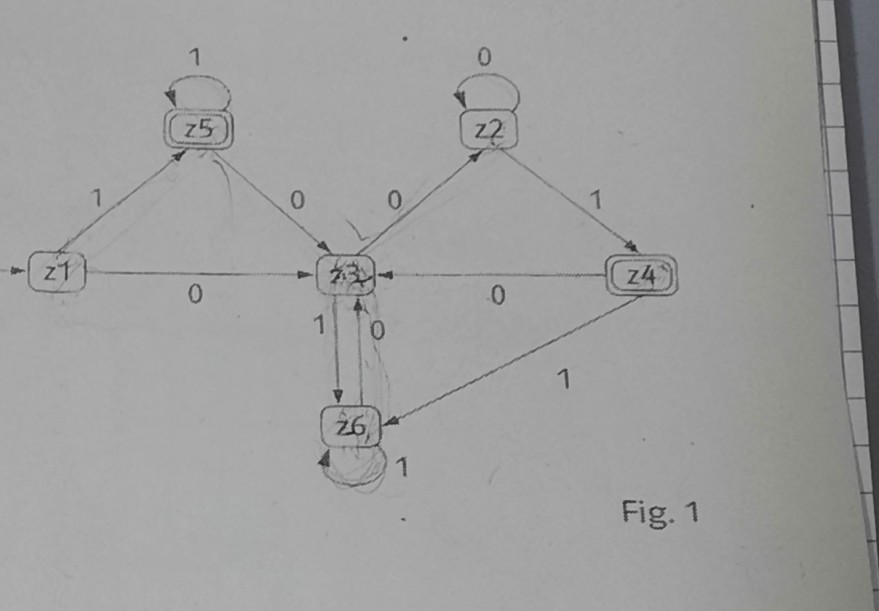
Das Bild ist der endliche Automat um den es sich in der Aufgabe handelt.
Text erkannt:
Fig. 1
Also bei Aufgabe A sollen wir gucken welcher der folgenden Nummern akzeptiert werden...
Meine Lösung:
Akzeptiert wird: 1111; 1001; 0010100
Nicht akzeptiert wird: 10101; 001101; 0101010
Stimmt das?
Aufgabe B lautet: formuliert allgemein, welche Wörter hier erkannt werden. Tipp: Betrachte die Endzustände und untersucht, wie die drei letzten Zeichen der akzeptierten Wörter aussehen.
Keine Ahnung. Meine Lösung wäre :
001 ; 10001; 11; 10011001
Keine Ahnung stimmt das? Habe ich das falsch verstanden ? Hier brauche ich aufjedenfall Hilfe. Ich denke wichtig ist, dass am Ende eine 1 muss oder ? Ich verstehe die nicht.
Letze Aufgabe: in eine Tabelle Formen
Meine Tabelle:
Aktueller Zustand Eingabe:0 Eingabe: 1
z1 z3 z5
z2 z2 z4
...
z5 z3 z6
Stimmt das so?
Vielen Dank für eure Hilfe